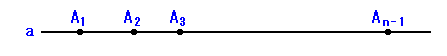n本の直線でn(n-2)/3個の三角形が出来る条件についての考察
0 前提条件
n(n-2)が3で割り切れる場合についての考察です。
1 準備
1-1 3直線以上が1点で交わることがない場合、2つの三角形が
同じ辺を共有することはありません。
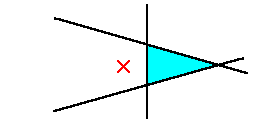
同じ辺を共有する三角形があれば、共有辺の端のうち
少なくとも1つは3直線以上が交わります。
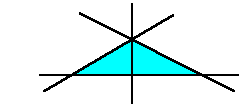
1-2 3直線以上が1点で交わる時、既存の交点に3本目の直線を
追加すると、線分が3本減ります。
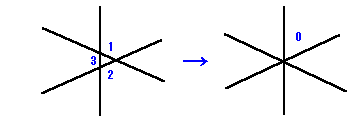
4本目はさらに5本、5本目はさらに7本と、減り方も大きくなります。
既存の交点に直線を追加した場合のみ、その両側で
辺を共有する三角形が作れますので、辺の数は最大2本
得します。
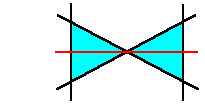
1本の直線が既存の交点を複数箇所通る場合は、
その交点毎に、線分が3本以上減り、辺の数が最大2本得します。
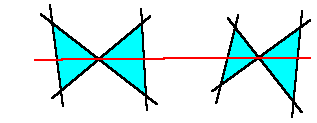
従って、3直線以上が1点で交わる箇所がある場合、辺の
総数は必ずn(n-2)より少なくなりますので、n(n-2)/3個の
三角形は作れなくなります。
1-3 n(n-2)個の線分を全て三角形の辺として使わなければならないため、
1つの線分は必ず三角形の辺となり、線分の片側が三角形、反対側が
三角形でない領域となります。

1-4 直線の端の交点を除き、交点を頂点とする三角形は、必ず対頂角を
使用する2つとなります。

三角形が2つ未満の場合、辺として使われない線分が出来てしまい、
三角形が3つ以上の場合や隣り合う場合は同じ辺を共有してしまうためです。
1-5 ある直線について、交点毎に三角形のある側が反転します。
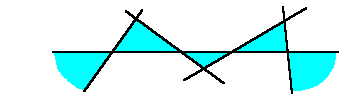
同じ側に連続して三角形が存在すると、辺を共有してしまい、
同じ側で連続して三角形が存在しないと、辺として使用されない
線分が出来てしまうためです。
2 本題
2-1 n本の直線のうち、ある直線a上のn-1個の交点をA1〜An-1とします。
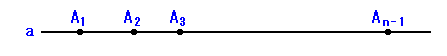
平行な直線や3直線以上の交点があると、辺の総数がn(n-2)に満たなくなりますので、
1本の直線には必ず残りn-1本の直線が異なる箇所で交わります。
2-2 An-1で交わる直線bを考えた場合、An-1のまわり4領域のうち三角形が出来る箇所は
線分An-2An-1の片側のみとなります。
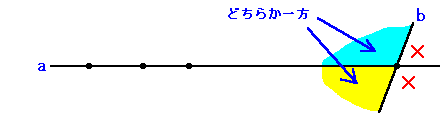
もし、直線aの端点が直線bの端点ではない場合、辺として使用されない線分が
出来てしまいます。
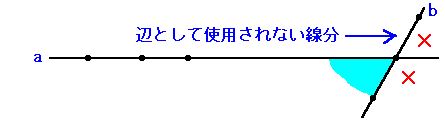
従って、aの端点は直線bでも端点(B1かBn-1)でなければなりません。An-1=B1 とします。
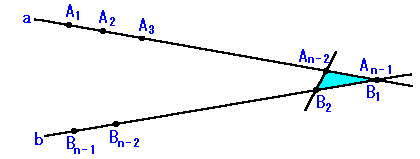
2-3 直線bのもう一方の端点は、同様に直線cの端点となります。
直線cはA1〜An-2のどれかを通らなければなりませんので、
直線a,b,cの関係は
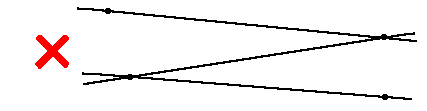
のようになることは出来ません。必ず
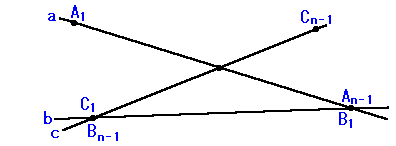
のようになります。
2-4 同様に続けていくと、いつかA1に戻ってきて、m本のループと
なります。
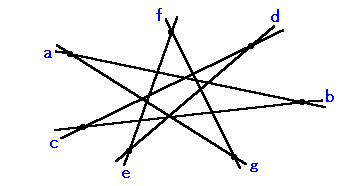
しかし、ループが2つ以上になることはありません。
なぜなら、このループの全ての直線と交差する直線は引けないからです。
(端点より外側で交わってはいけないことに注意。)
従って、ループは必ずn本全ての直線を使ったループとなります。
2-5 nが偶数の時、このループが作れませんので、n(n-2)/3個の三角形は出来ません。
また、A1A2を辺とする三角形と、An-2An-1を辺とする三角形は直線aの同じ側に
なければなりませんが、nが偶数ならば1つの直線の交点が奇数個になり、1-5のように三角形の
ある側が交互になることからも、nが偶数では不可能であることがわかります。
n=6,n=8の時にn(n-2)/3個の三角形は作れないわけですね。
2-6 例えば7本の直線でループを作るとき、
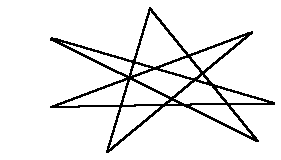
の他に
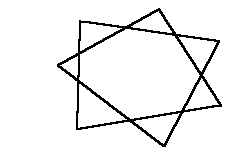
のようなパターンも思い付きますが、これは全ての直線同士が交差しませんので
n(n-2)/3個の三角形が作れません。必ず内角の和が180°になるようにループする
必要があります。従って、例えばn=21の場合に最大数の三角形となるのは、
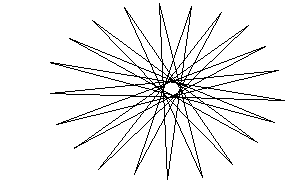
というパターンを頂点の回る順番を変えないように変形したものに限られます。
n=15で三角形65個のこの図も、最初に上のような図を作ってから
頂点を移動することにより作ったものです。
3 発展
発展…とか書きながら、今のところこれ以上のことはわかっていません。
図形内部で三角形になっていない領域は必ず五角形または六角形で
なければならないようですが、今のところ本当にそうなのか、
またどういう理由によるものかなど、全然わからない状態です。
上記の理論で、とりあえず理論的に1,2,5,7,11,15,21が最大であることは
示せたと思いますが、n(n-2)が3で割り切れない(必ず2余る)場合は
さらに難しく、n=10の時に線分を5本も無駄にしなければならないのは
本当か、またはなぜか、ということまではまだ考えが及んでいません。
暇をみてもう少し考えてみたいと思います。