仮俙俛俠偵偍偄偰丄佢俛亖俁侽並丆俛俠亖侾亄 |
丆俙俠亖 |
偱偁傞丅巆傝偺曈丄妏傪媮傔傛 |
椺戣偺儁乕僕 |
| 丂 |
|
| 丂夝摎椺偺慜偵堦尵 |
| 丂丂丂偙偺栤戣偵尷傜偢丄悢妛偱偼傑偢恾傪昤偄偰奣宍傪攃埇偡傞偙偲偑戝愗偱偡丅偮傑傝丄 丂丂丂庤傪摦偐偟偰丄栚偱尒偰僀儊乕僕傪偮偐傫偱丄摢偱峫偊傞丅 |
| 丂 |
 |
|
| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偺傛偆偵丄偁傞掱搙惓妋側恾傪昤偔偙偲偱丄偩偄偩偄偺宍偑捦傔傑偡丅 夝摎椺 |
| 丂丂丂佢俛傪梡偄傞梋尫掕棟偐傜丂丂俀亖(侾亄 | ) | 2 | 亄俙俛 | 2 | 亅俀(侾亄 | )俙俛們倧倱俁侽並 |
| 丂丂丂丂丂丂傛偭偰丄俙俛 | 2 | 亅(俁亄 | )俙俛亄俀(侾亄 | )亖侽丂丒丒丒嘆 |
| 丂丂丂丂丂丂丂丂丂丂嘆偺傛偆側宍(AB偵偮偄偰崀傋偒偺弴)偵惍棟偡傞偲偒丄傓傗傒偵揥奐 |
| 丂丂丂丂丂丂丂丂丂丂偟偰偼偄偗側偄丅俙俛 | 2 | 偺崁丄俙俛偺崁丄掕悢崁偲暘偗偰寁嶼偡傞丅 |
| 丂丂丂丂丂丂丂丂丂丂傑偨丄嘆偼場悢暘夝偱偒傑偡丅 |
丂丂丂丂丂丂丂(俙俛亅俀)(俙俛亅侾亅 |
)亖侽丂丂傛偭偰丂俙俛亖俀丆侾亄 |
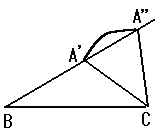
丂丂丂忋偺恾偐傜丂俙俛亖俀偺偲偒丄揰俙偼俙乫偵側傝丄俙俛亖侾亄 |
偺偲偒丄揰俙偼俙乫乫偵側傞丅 |
| [嘥]丂俙俛亖俀偺偲偒丂丂俙乫偐傜俛俠偵悅慄傪堷偔偲丄撪妏偑丂俁侽並丆俇侽並丆俋侽並偺捈妏嶰妏宍偲丄 丂丂丂丂丂丂丂丂丂丂丂丂丂丂係俆並丆係俆並丆俋侽並偺捈妏嶰妏宍偑偱偒傞偺偱丂佢俠亖係俆並丄佢俙亖侾侽俆並 |
| [嘦]丂俙俛亖侾亄 | 偺偲偒丂嶰妏宍俙俛俠偼俙俛亖俛俠偺擇摍曈嶰妏宍偵側傞偺偱丂佢俠亖佢俙亖俈俆並 |
[嘥]偲[嘦]偱丄巆傝偺佢俙丆佢俠傪媮傔傞偲偒偵惓尫掕棟丒梋尫掕棟傪棙梡偟側偄傛偆偵 ! ! 娙扨偵媮傔傟傞曽朄傪尒偮偗弌偡偙偲偑悢妛偺幚椡傪崅傔傑偡丅 |
| 丂 |
|