日本数学教育学会秋期研究大会（高知・広島・福岡）の投稿論文（2020〜2022）
をダウンロードする(PDFファイル)

 　　　いかにして真なる全称命題を創るか
−全称命題の証明の再考と「課題学習」の素材研究を通して−
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　中谷　清茂
　　　　　　　　　　　　　　　　　　　　　　　　　　中谷塾経営者＆講師
　　　「解く」数学から「創る」数学へ

帰納→予想→（反例・修正）→証明→定理→拡張命題→（反例・修正）→証明→拡張定理

定理の創り方（本稿の「中谷の第一定理」の証明を具体例として）※略証

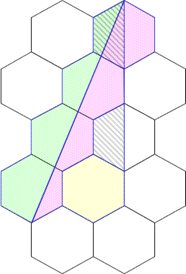
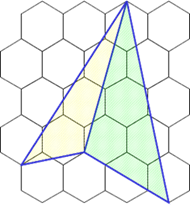
Ｓ_１＝ｍ＋ｎ／２… が成り立つ．                      ※右図のように
　 Ｓ_１：格子多角形の面積                          　　　２つの三角形が接合している時
　 　ｍ：格子多角形内にある完全な格子枠数　         境界線を含む互いの格子枠は，
       ｎ：１辺と格子枠で囲まれた図形数               　　加法性が成り立つ．
　※２辺と格子枠で囲まれた図形は数えない．  　　上から，・０＋０＝０
　　左図ではＳ_１＝ｍ＋ｎ／２　　　　 　　　　　 　　・１／２＋０＝１／２ 
　　　　　　　　＝１＋４／２　　　　　　　　　　　　　・１／２＋０＝１／２
　　　　　　　　＝３　　　　　　　　　　　　　　 ・１／２＋１／２＝１

※図と式を観ていると「額賀の定理」の幾何的証明とコラボする．（「クレセール」参照）