n本の直線でn(n-2)/3個の三角形が出来る条件についての考察(2)

※以下の説明で、「端点」とはある直線の最初または最後の交点のことを
　示します。前の説明の A₁, B₁, C₁, …のことです。


4　nが6以上で3の倍数でない時にn(n-2)/3個の三角形が作れない理由


4-1　n(n-2)/3個の三角形が作れる場合、端点を含む三角形は
　　ちょうどn個ありますが、その三角形について考えます。

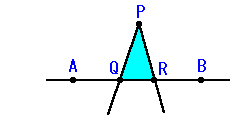
　　Pは端点です。n＞3であれば、QやRが端点になることはありません。

(1) AとBが両方とも端点の場合
　　これはn=5の場合です。n≠5ではあり得ません。

(2) AとBが両方とも端点でない場合
　　局所的には、必ず以下のようになり、端点を含む他の三角形と隣接しません。


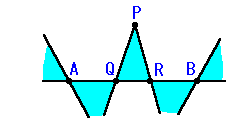
(3) AとBのどちらか一方が端点の場合
　　必ず以下のようになり、端点を含む他の三角形と共有頂点で隣接します。

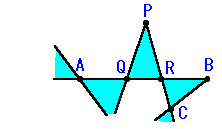
　　ただし、端点を含む三角形が3つ以上隣り合うのは、(1)のように
　n=5の場合だけで、n＞5では2つのみです。
　　従って、n＞5の場合、端点を含む三角形は(2)か(3)のどちらかのパターンと
　なります。以下、特に断らない限りn＞5とします。


4-2　(3)のパターンに対して、(2)のパターンが必ず一つ対応します。

　端点を含む三角形が隣り合う場合、共有頂点を通らない2本の直線は
必ず反対側の端点で交わります。

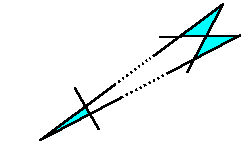
　この反対側の端が、2つの三角形が隣接しているうちの一つとなることは
ありません。

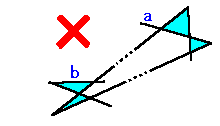
　なぜなら、このようになった場合、上図のaとbは同一直線でなければ
ならないため、

のように、端点を含む三角形が3つ以上隣り合ってしまうためです。
このようになるのは、n=5の場合だけです。
　従って、(3)のパターンに対して、(2)のパターンが必ず一つ対応します。


4-3　(3)のパターンに対応しない(2)のパターンは存在しません。

　もし、(2)のパターンの反対側の一つが(2)のパターンだったとします。

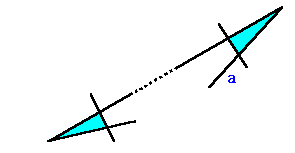
　すると、aの反対側は(3)のパターンにはなることが出来ませんので、
再び(2)のパターンとなります。

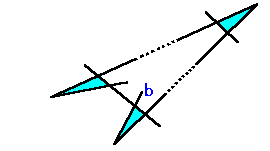
　bの反対側も(2)のパターンになり、そのまた反対側も(2)のパターンに
なり、これがずっと続きますので、(2)のパターンだけでループを構成
し、(3)のパターンは一つもないことになります。
　しかし、これは明らかに成り立ちません。端点を含む三角形を全て削除
した図形を考えるとわかりますが、その図形の凸頂点となれるのは
(3)のパターンの箇所だけです。
　例えば、n=9の この図では、端点を含む9個の三角形を除いた図形は
三角形であり、3つの凸頂点は(3)のパターンとなっています。
　また、n=15の この図では、端点を含む15個の三角形を除いた図形は
☆型であり、やはり5つの凸頂点が(3)のパターンとなっています。

4-4　4-2と4-3により、(2)のパターンと(3)のパターンは一対一に対応することが
　　わかりました。

　　(2)のパターンと(3)のパターンで端点が3つですので、端点3つずつで組となります。
　　以上により、nが3の倍数でない場合は三角形がn(n-2)/3個になるパターンは
　作れないことになります。


　n=11は3の倍数ではありませんので、11(11-2)/3=33個の三角形は作れません。
三角形が32個になるパターンは既に見つかっていますので、n=11の場合の
三角形の個数の最大は32であることがわかりました。

　今までわかっていることにより、三角形の個数の上限は
　　・nが5または3の奇倍数の時は n(n-2)/3 個
　　・それ以外の時は [{n(n-2)-1}/3] 個
となり、具体値は

n	3	4	5	6	7	8	9	10	11	12	13	14	15	16
上限	1	2	5	7	11	15	21	26	32	39	47	55	65	74

となります。緑は確定、赤は未確定です。

　n=10の時は最大25個とほぼ確信していますが、今のところ確定出来る理由が
わかっていません。ただ、上記のことからもう少し推論を進めるとわかりそうな
気がしますので、引き続き考えてみます。