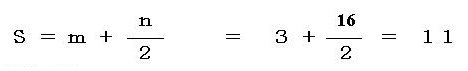since2002.10since1999.12 yesterday today
final renewal day 　2006.1.17　　　　　　　　　　　　　　　　　　　　　　To Japanese

　　　　Mathematics : a new theorem.
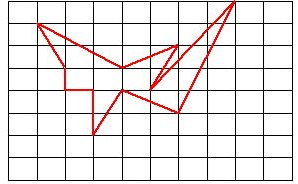
　　 It answers easily 【 anyone 】 【 the area of the lattice polygon 】.
-----The answer of the area of the bottom figure is made of about 10-second (junior high school student).-----

　　　　　　　　　　　　　　

1, The name of the theorem.　　　　　　　　　　　　　　　　　　　　　
　　　Nukaga's theorem.
　
2, The discoverer of the theorem.
　　 Hiroshi Nukaga
　　 It is a school teacher with the Japanese.(The present: Hokota　minami Junior　high school)
　
3, Working school of the time when a theorem was discovered, and those days.
　　August, 1990
　　Ibaraki Prefecture Kashima town-run Kashima junior high school working age.
　　(Incumbent : deer Kashima city Kashima junior high school).

4, The proof person (three people ; 3ways) of the theorem.
　　* Hiroshi Nukaga. discoverer said person. : Inductive proof.
　　* Mr. Kiyoshige Nakaya (Nagano Prefecture junior high school teacher) Geometrical proof.
　　* Mr.Yasuhisa Hirai (teacher of Okayama university) Algebra-like proof.

to Proof←　please click on here

5, The formula of the theorem and the calculation example which the answer of the area of the lattice polygon of the upper figure is worked out to.
　　　　　

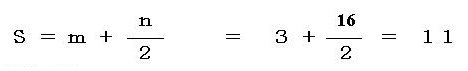
Formula
　　S = m ＋ n ／ 2　

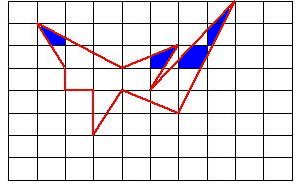
　　S : The area of the lattice polygon.
　　m: The number (the pink frame of the bottom figure) of the perfect frame (square frame).
　　n: The number (the green frame of the bottom figure) of the frame (the frame that it is surrounded in one imperfect side and the lattice frame).The frame which is not a square.
　　p: The frame (the blue frame of the bottom figure) that it is surrounded in two sides which are not in the line top of the lattice frame, and the lattice frame.This frame is not a square, either.
　　　
　　　To the child student, "There are two sides in the frame, and the frame coming to find the area of that isn't counted." When it said and a board document did a picture, children to the third grade in the junior high school from the fifth grade in the elementary school understood it fully.

　
　 As much as it counts the number of frames of "m" "n" and it substitutes it for the above formula and it is calculated.
　　　Attention : The frame of "p" isn't counted.
　　　　　　　　　In other words, the frame of "p" is ignored at all.
　　　　　　　　　This is the point of Nukaga's theorem.
　
6 The method (One lattice is made 1 unit area.) that the area of the lattice polygon answers it.　
　
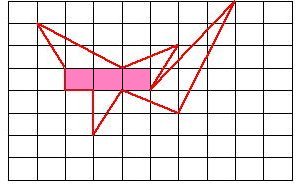
　　　 m: A perfect frame (a pink frame), three. m = 3

　
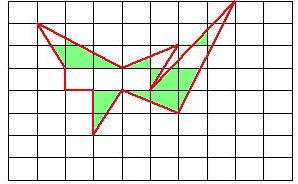
　　　n: An imperfect frame (a green frame), 16. n = 16

　
　　p: The frame (a blue frame) which isn't counted, five. p = 5

　 S=m+n/2=3+16/2 =3+8=11 It becomes the area which is and which is the same as the lattice frame (square) for 11.

　A lattice frame doesn't need to be a square.
　A answer becomes 11c ㎡ if 1 lattice frame is 1c ㎡.
7. Relation with other theorems.(It answers easily 【 the area of the lattice polygon 】.)

　　There is worldwide famous "the theorem of Pick".
　　The number of points of the lattice polygon is counted, and it answers as for "Pick's theorem" 【 the area 】.

　　The number of frames of the lattice polygon is counted, and it answers as for "Nukaga's theorem" 【 the area 】.
　　Therefore, as for the lattice polygon, it decided to answer in these two methods 【 the area 】.

8. How to deal with it in the class.

　　*The introduction of "the theorem of 3 square" of the third grade in the junior high school.
　　*Subject solution learning.

I wrote this home page using Translation software.