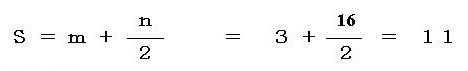since2002.10
since1999.12
最終更新日 2017.11.10 To English 英語の解説のページへ
数学の新しい定理(Mathematics : a new theorem.)
格子多角形の面積を簡単に求められる
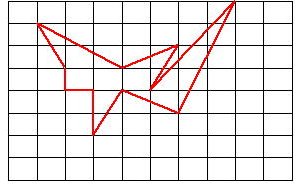
-----下図の面積を求めるのに，十数秒（中学生）で求まります-----
１ 定理の名称
額賀の定理（ぬかが の ていり）
２ 定理の発見者
額賀 博（ぬかが ひろし） Hiroshi Nukaga
(H30年度 茨城県鉾田市立上島西小学校長 )
３ 定理を発見した時期と当時の勤務校
平成２年８月
茨城県鹿島町立鹿島中学校勤務時代(現:鹿嶋市立鹿島中学校)
４ 定理の証明者(3人；3通り)
額賀 博 発見者本人 帰納的な証明
中谷 清茂 先生(元長野県中学校教諭） 幾何学的な証明
平井 安久 先生 (岡山大学） 代数的な証明
証明のページへ 証明は左記をクリックして下さい。
５ 定理の公式と上記の格子多角形の面積を求める計算例
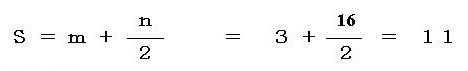
S = m ＋ n ／ 2
Ｓ：格子多角形の面積
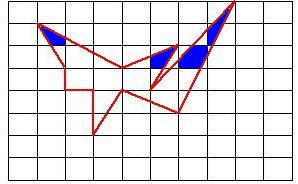
ｍ：完全な枠（格子１マス）の数(下図のピンクの枠）
ｎ：不完全な枠（１本の辺と格子枠に囲まれている枠）の数(下図のグリーンの枠）
ｐ：格子枠の線上でない２本の辺 と 格子枠に囲まれている枠(下図のブルーの枠）
児童生徒には「枠の中に2本のへんがあって，その中の面積を求めるようになっている枠は数えない。」
と言って絵を板書したところ小学校5年生～中学3年生は十分理解してくれました。
面積はｍ,ｎの枠の数をかぞえて公式に代入して計算するだけ｡
注意：ｐの枠を数えない。つまり,ｐの枠は全く無視する。ここが額賀の定理のポイントです。
６ 格子多角形の面積の求め方（格子1マスを１単位面積とする）
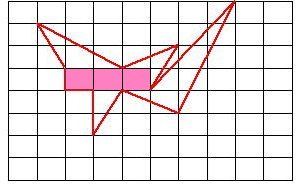ｍ：完全な枠 (ピンクの枠）が3個
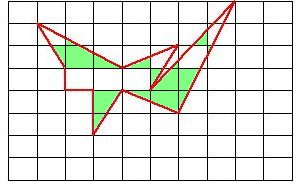ｎ：不完全な枠 (グリーンの枠）が16個
ｐ：数えない枠 (ブルーの枠）が5個
Ｓ ＝ ｍ ＋ ｎ／２ ＝ ３ ＋ １６／２ ＝
３ ＋ ８ ＝ １１ となり 格子が11個分の面積となる。格子は正方形でなくてもよい。
格子1マスが １cm × １cm ＝ １ c㎡ (平方センチメートル） であるなら， 答え １１
c㎡ (平方センチメートル） となる。
７ 格子多角形を求める他の定理との関連
世界的に有名な 「 ピックの定理 」 がある｡
この定理は格子多角形の点の数を数えて面積を出す。
「 額賀の定理 」は，面を数えて面積を出すので，格子多角形はこれらの2通りの方法で面積を求められることとなった。
8 授業での扱い
・中学3年生の｢三平方の定理｣の導入
･課題解決学習
