10本の直線で26個の三角形が作れない理由
以前のページ
n本の直線でn(n-2)/3個の三角形が出来る条件についての考察
n本の直線でn(n-2)/3個の三角形が出来る条件についての考察(2)
5 10本の直線で26個の三角形が作れない理由
25個は作れることが既にわかっていますので、26個が作れないことを示せば
最大値が25個と決まります。
それには、辺の総数がn(n-2)=80より3本以上は少ないことを示せば十分です。
5-1 4直線以上が1点で交わる場合は考える必要がありません。
4直線が1点で交わると、交わらない時と比較して線分が7本少なくなり、
得する辺の数は最大4つで、全体の辺の数は少なくとも3本減って26個の三角形は
作れなくなります。
従って、3直線以上が1点で交わる場合はあっても、4直線以上を考える必要は
ありません。
5-2 3直線の交点は、最大2個と仮定して問題ありません。
3直線の交点1個毎に、辺が少なくとも1つ減ります。従って、3直線の交点が
3個以上あると26個の三角形は作れなくなりますので、3直線の交点は最大2個
と仮定出来ます。
5-3 3直線の交点が3個以下であれば、平行線はないと仮定して問題ありません。
もし平行線を使って26個の三角形が作れた場合、平行線上に3直線の交点が
なければ、平行線を微妙にずらして平行でなくしても、三角形の個数は変わりません。
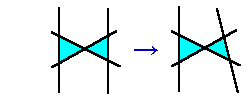
また、平行線上に3直線の交点が1つあっても、その交点を中心として微妙に回転
すれば平行でなくなりますから、平行線をなくすことが出来ます。
平行線に3直線の交点が2つある場合はそうはいきませんが、3直線の交点が
3個以下ならば、平行線のうち3直線の交点を2つ以上含む直線は1本だけですので、
それ以外の平行線を動かせば平行でなくすることが出来ます。
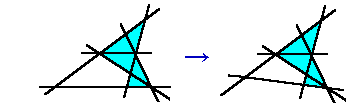
従って、平行線はないと仮定して問題ありません。
5-4 平行でない10本の直線を引いた時、ある直線は他の9本全部の直線と交わり、
各直線において“両端の交点”(以降、端点と表します)が決まりますが、
端点は3直線の交点ではないと仮定して問題ありません。
もし、端点が3直線の交点であった場合、
そのうちの1本を微妙にずらせば、
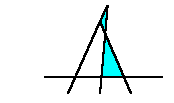
三角形の個数を減らさずに3直線の交点をなくすことが出来ます。
従って、端点は3直線の交点ではないと仮定して問題ありません。
5-5 3直線の交点を含まない直線は、辺とならない線分を作ります。
もし、いずれかの端点が他の直線の端点でない場合は、その端点に隣接する線分の
どちらか1つが辺にならない線分となります。
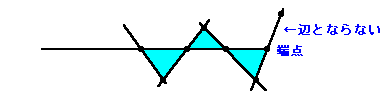
両端が他の直線の端点である場合は、
(a) 端の線分が三角形を作っていなければ、それは辺とならない線分です
(当り前です)。
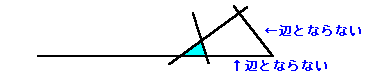
(b) 両端の線分が三角形を作っていれば、それはその直線の同じ側にあります。

なぜなら、もし反対側にあった場合、
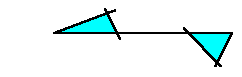
平行線はありませんので、それは実は端点同士の交点ではないからです。
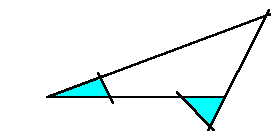
(c) 3直線の交点を含まない直線では、1つの線分の両側が三角形となることは
ありません。従って、両端の三角形が直線の同じ側で、線分の個数が8個ですから、
三角形の辺となっていない線分があるか、
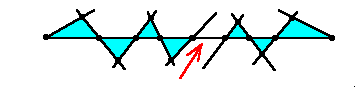
あるいは三角形が片側に2個連続している箇所があるか
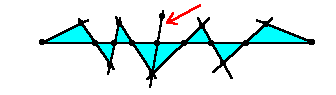
のどちらかとなり、いずれの場合でも辺として使用されない線分(赤矢印)が
存在することになります。
ただし、1つ例外があります。
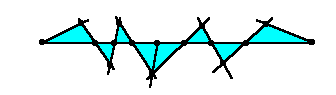
のように、三角形が片側に2個連続していて、その間の点が端点だった場合です。
この場合だけは、辺とならない線分は出来ません。
3直線の交点をうまく使うと、損が減るということです。n=8がいい例ですね。
5-6 また、辺とならない線分は、3直線の交点を含まない直線1本あたり1本という
わけではありません。
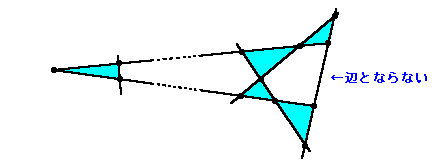
このように、2本あたり1本となる可能性もあります。
しかし、関係するのは辺とならない線分の端を通る直線だけですので、
「2本あたり1本」が最大で、3直線の交点を含まない直線が3本あれば、
(辺が減らない例外を除けば)辺とならない線分が最低2本出来ます。
5-7 以上により、辺が少なくとも3本減ることがわかります。
(a) 3直線の交点が2つの場合
3直線の交点を含む直線は最大6本ですから、3直線の交点を含まない直線が
最低4本あります。このうち2本は例外により辺が減らない可能性がありますが、
残りの2本で必ず辺とならない線分が最低1本出来ますので、辺は最低3本減ることに
なります。
(b) 3直線の交点が1つの場合
3直線の交点を含む直線は3本ですから、3直線の交点を含まない直線は7本で、
例外分1本を除いても辺とならない線分は少なくとも3つ出来ますので、
辺は最低4本減ることになります。
(c) 3直線の交点がない場合
3直線の交点を含まない直線は10本ですので、辺は最低5本減ることになります。
いずれの場合も、辺は少なくとも3本減りますので、26個の三角形を作ることは
出来ないということがわかりました。
6 n=8の時、3直線の交点がないと15個の三角形が作れない理由
「n=10で26個」を検討したことによって、この理由もわかりました。
上と同様の理屈で、3直線の交点がない場合は3直線の交点を含まない直線は
8本ですので、辺は最低4本減り、8×(8-2)-4=44<15×3ですから、15個の
三角形は作れないことになります。
nが偶数で3直線の交点がない場合の上限は[{n(n-2)-n/2}/3]となりますが、
これをいくつか表にしてみると
| n | 4 | 6 | 8 | 10 |
12 | 14 |
| 上限 |
2 |
7 |
14 |
25 |
38 |
53 |
のようになります。
n=4,6,8,10の中では、たまたまn=8だけその条件に該当していたわけですね。
nが大きい偶数の時、例えばn=50とすると、3直線の交点の個数に対して上限が
| 3直線の交点の個数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 上限 |
791 |
792 |
792 |
792 |
793 |
793 |
793 |
794 |
794 |
794 |
795 |
795 |
795 |
のように変化します。他にも上限を抑える要素があるかも知れませんので可能性の
話ですが、nが偶数で大きい場合は3直線の交点がたくさん必要なのかも知れません。
また、3直線の交点が有利に働くのは、nが偶数の場合のみです。1本の直線上の
線分が偶数個で、三角形のある側が合わなくなるのを調整する働きになります。
nが奇数の時は、逆に不利に働きます。実際、n=4,6,8,10はいずれも3直線の交点が
あって最大値をとることが出来ますが、逆にn=3,5,7,9はいずれも最大値をとれなく
なっています。これは以前の調査で予想していた通りですね。
8 ここまでのまとめ
今までの調査結果により、三角形の個数の上限は
・nが偶数の時は [{n(n-2)-[(n+2)/4]}/3] 個
・nが5または3の奇倍数の時は n(n-2)/3 個
・それ以外の時は [{n(n-2)-1}/3] 個
となりました。
(※5-1,5-3の条件は多分無視出来ると思いますので、ここでは無視しています。)
これであらためて表を作ってみると、
| n | 3 | 4 | 5 | 6 |
7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 |
| 上限 |
1 |
2 |
5 |
7 |
11 |
15 |
21 |
25 |
32 |
39 |
47 |
54 |
65 |
73 |
のようになります。緑は確定、赤は未確定です。
この先は確率的試行では厳しいですね。相当試行しないと、n=12で
三角形39個は得られなそうです。もしかしたら、今までわかったことを
考慮しながら、手作業で考えた方が早いかも知れませんね。