微分と積分

１９世紀後半から発展してきた微分･積分は数学史上最大の発見といわれています。この発見がなかったら
現在のような便利な生活はおそらくないでしょう。理系進学者にとっては、とても大切な分野なので、本質を見
極めるように心して学習してください。（ここでは、全ての区間で微分可能として説明しています。）


高校の物理の授業でまず、　　Ｖ＝Ｖｏ＋α ｔ　・・・・［ア］，Ｘ＝Ｘｏ＋Ｖｏｔ＋ １
２		 α ｔ 2

 　・・・・［イ］　
　　　　　　　　　の式を習った覚えがあると思います。この2つの関係式は、まさに微分と積分なのです。
　　　　　　　　　（なお、［イ］の関係式で、Ｘｏ＝０　であつかう場合もあります。）
　　　　　　　［ア］→［イ］が積分で、［イ］→［ア］が微分です。つまり、微分と積分は互いに逆演算 なのです。
　数学ＩＩＩ・物理ＩＩ の範囲になりますが、単振動の　Ｘ＝Ａｓｉｎω ｔ　，　Ｖ＝Ａω ｃｏｓω ｔ　も同様です。

話が物理の分野になっていますが、もともと運動の解析から進歩してきた分野なので、頭が痛いかも知れ
ませんが、もう少し辛抱してください。［［ア］，［イ］についての説明。］

中学３年生で二次関数を習ったときのことを思い出してください。「落下運動の平均の速さ」　という内容を
覚えていますか？　「平均の速さ」の考え方が微分の基になっています。
左の図は、Ａから物体を落下させたときのモデル図です。いま各点の間隔は０．１秒とします。
また、各点の座標を、ＸA，ＸB，ＸC，ＸD，ＸE，とします。

　　　　　　ＡからＥまでの平均の速さは、（ＸE－ＸA）÷０．４
　　　　　　ＢからＥまでの平均の速さは、（ＸE－ＸB）÷０．３
　　　　　　ＣからＥまでの平均の速さは、（ＸE－ＸC）÷０．２
　　　　　　ＤからＥまでの平均の速さは、（ＸE－ＸD）÷０．１ 　　　　　と表せます。
いま、点Ｅを固定して、他の点を徐々に点Ｅに近づけています。さらに、点Ｄと点Ｅの間に点を考えて、
同じように平均の速さを考えると、点Ｅの瞬間の速さになります。
　　　　　　　　記号で表すと、 　 ｌｉｍ
Δｔ→0		 （ＸE＋ΔＸ）－ＸE
　　　　Δｔ		 　・・・［＊］　　となります。

　　　　　　　　　　　　ここで、ΔＸ はＸEからの変位，Δｔ　はその間の時間で、
　　　　　　　　　　　　　　　ＸEより前の地点ならば、ΔＸ ＜０，Δｔ ＜０　
　　　　　　　　　　　　　　　ＸEより後の地点ならば、ΔＸ ＞０，Δｔ ＞０　となります。
　　　　　これが微分の考え方の原点です。
　　　　　　次に横軸に時刻、縦軸にこの物体の位置のグラフを考えると、
　　　　　　　　［＊］は点（ｔE，ＸE）における接線の傾きになります。
　　　　　　　　　　（この部分の細かい説明は教科書を見直してください。）
関数 ｆ（Ｘ） について、 ｌｉｍ
ｈ→0		 ｆ（Ｘ＋ｈ）－ｆ（Ｘ）
　　　　ｈ		 　　が存在するとき、これを　　 ｆ’（Ｘ） とか、 ｄｆ（Ｘ）
　ｄＸ		 　と表します。
　　　　この計算を「ｆ（Ｘ）を微分する」といい、その結果の関数を「導関数」といいます。
　　　　　　　　　　　また、この導関数に、数値を代入した結果を「微分係数」といいます。
　　　　微分係数を利用して、接線の方程式を求めることが出来ます。

　　　　関数 Ｙ＝ｆ（Ｘ）　上の点 （ａ，ｆ(ａ)）における接線の方程式は
　　　　　　　　　　　　　　Ｙ－ｆ（ａ）＝ｆ’(ａ）（Ｘ－ａ）　　となります。（直線の方程式参照）
　　　　　　　　　　　　　　　　　　　　

では、ｆ’（Ｘ）の求め方です。ただし、ａ≠０，ｎは自然数とします。
数学ⅡＢでは整関数だけをあつかうので、ｆ（Ｘ）＝ａＸ n　について考えます。二項定理を用いて、
　　　　　　　ｆ（Ｘ＋ｈ）－ｆ（Ｘ）＝ａ（Ｘ＋ｈ）n－ａＸ n
　　　　　　　　　　　　　　　＝ａ（nＣ1Ｘ n-1ｈ＋nＣ2Ｘ n-2ｈ2＋・・・＋nＣn-1Ｘ ｈn-1＋nＣnｈn）

　　　よって、 ｌｉｍ
ｈ→0		 ｆ（Ｘ＋ｈ）－ｆ（Ｘ）
　　　　ｈ		 ＝ ｌｉｍ
ｈ→0		 ａ（nＣ1Ｘ n-1＋nＣ2Ｘ n-2ｈ＋・・・＋nＣn-1Ｘ ｈn-2＋nＣnｈn-1）＝ａnＣ1Ｘ n-1

　　　　　より　　ｆ（Ｘ）＝ａＸ n　の導関数　ｆ’（Ｘ）＝ａｎＸ n-1 　　となる。
　　　　　これは、全ての自然数について成り立つので、多項式についても単項式の和として扱えます。

逆に、ｆ’（Ｘ）＝ａｎＸ n-1 となるような ｆ（Ｘ）　はどのような関数でしょうか？
　　　　　　　「定数を微分すれば ０ になる」　このことに注意すれば、
　　　　　　　ｆ（Ｘ）＝ａＸ n ＋１，ａＸ n ＋２，ａＸ n ＋３，・・・・　と　いくらでも考えれます。
　　　　　ですから、適当な文字を用いて
　　　　　　　　　ｆ（Ｘ）＝ａＸ n ＋Ｃ　　　とあらわします。このＣを積分定といいます。

　　　積分は、微分の逆演算であることをしっかり理解して下さい。

もう一つ積分で大切なのが面積の理解です。

関数 Ｙ＝ｆ（Ｘ） がつくる図の斜線の面積について考えます。
左の図を参考にして下さい。斜線の面積をΔＳとすると、
　　ΔＸ・ｆ（Ｘ）＜ΔＳ＜ΔＸ・ｆ（Ｘ＋ΔＸ）　・・・［＊］
ここで、二点（Ｘ，ｆ（Ｘ）），（Ｘ＋ΔＸ，ｆ（Ｘ＋ΔＸ））を通る
直線の傾きをｍとすると、ｆ（Ｘ＋ΔＸ）＝ｆ（Ｘ）＋ｍΔＸ
となるので、不等式［＊］は
　ｆ（Ｘ）＜ ΔＳ
ΔＸ		 ＜ｆ（Ｘ）＋ｍΔＸ　となり、ΔＸ→０　とすると、
Ｓ’＝ｆ（Ｘ）　が成り立つ。

数学Ⅱまでの段階では少し難しいかもしれませんが、数学Ⅲではよく使います。
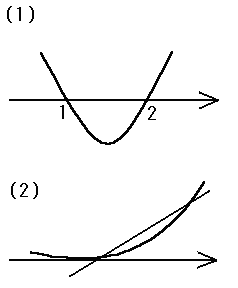
　　　　この内容はなかなか理解しづらいと思います。
　　　　とりあえず、Ｘ軸に垂直な線分の長さを積分すすれば面積になることを理解して下さい。
　　　　（積分は寄せ集めることなので、線分が集まることで領域が出来るということです）

では、次の二つの面積について考えてみましょう。
まず、（１）Ｙ＝Ｘ 2 －３Ｘ＋２　と　Ｘ軸の囲む面積　　（２）Ｙ＝Ｘ 2 　と　Ｙ＝３Ｘ－２　の囲む面積
（２）の図は領域を誇張しています。
（１）では、 2
1		 －（Ｘ 2

 －３Ｘ＋２）ｄＸ 　（２）では、 2
1		 ｛（３Ｘ－２）－Ｘ 2

 ｝ ｄＸ

を計算すれば面積を求めることが出来ます。
図で（１）と（２）の領域は全く違いますが、計算式が一致していることに着目
して下さい。この例のような直線と二次関数が囲む面積は、その交点を
求める関数とＸ軸が囲む面積になることを知っておいてください。また、
二次関数だけでなく、他の関数についてもこのことはいえます。

面積は、どちらも　 １
６		 　です。
便利な公式
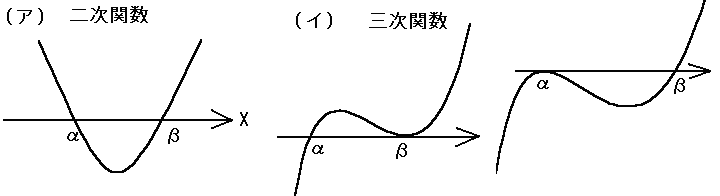（ア）この二次関数が、Ｙ＝（Ｘ－α）（Ｘ－β）と表せるとき、
　　　　　　Ｘ軸と囲む面積は、　　 β
α		 －（Ｘ－α）（Ｘ－β）ｄＸ ＝ （β－α）3
　 ６		 　となります。
（イ）この三次関数が、Ｙ＝（Ｘ－α）（Ｘ－β）2>と表せるとき、
　　　　　　Ｘ軸と囲む面積は、　　 β
α		 （Ｘ－α）（Ｘ－β）2ｄＸ ＝ （β－α）4
　 １２		 　となります。
　　　この三次関数が、Ｙ＝ａ（Ｘ－α）2（Ｘ－β）と表せるとき、
　　　　　　Ｘ軸と囲む面積は、　　 β
α		 －（Ｘ－α）2（Ｘ－β）ｄＸ ＝ （β－α）4
　 １２		 　となります。
　　　　　　　　　　　　　＊　この計算方法の説明は、例題のページに示します。



　　 　　 　 　　 　
微分の例題
積分の例題